Introduction
A Confidence Interval (CI) is a range of values that we believe, with a certain level of confidence, includes the true value of a parameter (like the average or proportion) in a population. Confidence intervals are commonly used in statistics because they help us understand the accuracy of our estimates.
Key Components of Confidence Intervals
- Point Estimate: This is our best guess of the population parameter. For example, if we surveyed a sample of people to find the average height, the average height from our sample is the point estimate for the population’s average height.
- Confidence Level: This tells us how confident we are that the interval contains the true population parameter. Common confidence levels are 90%, 95%, and 99%. A 95% confidence level means if we repeated the same sampling process many times, 95 out of 100 intervals would contain the true population parameter.
- Margin of Error: The margin of error is added and subtracted from the point estimate to create the interval. It depends on the variability of the data and the size of the sample.
How to Calculate a Confidence Interval
For a simple example, let’s say we’re estimating the average (mean) value of something, like the average height in a sample of students:
Find the Sample Mean: This is your point estimate. Let’s say the average height of students in your sample is 170 cm.
Determine the Standard Error: The standard error (SE) measures how much variability there is in the sample mean and can be found with the formula:
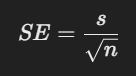
where ( s ) is the sample standard deviation, and ( n ) is the sample size.
Choose a Z-Score (or T-Score): For a 95% confidence interval, the Z-score is typically 1.96. This number comes from the standard normal distribution and corresponds to the desired confidence level.
Calculate the Margin of Error:

Construct the Confidence Interval: Finally, add and subtract the margin of error from the sample mean to get the confidence interval.

Interpreting the Confidence Interval
Suppose we calculated a 95% confidence interval of [168 cm, 172 cm] for the average height. This means we are 95% confident that the true average height of the population lies between 168 cm and 172 cm.
Why Confidence Intervals Are Useful
- Measure of Accuracy: They give a range within which we can reasonably expect the true parameter to fall, helping us gauge the accuracy of our estimate.
- Decision-Making: Confidence intervals can help in decision-making. For example, in quality control, if the confidence interval for the mean weight of a product is outside the acceptable range, it may indicate an issue with production.
- Comparing Populations: Confidence intervals help compare two populations. If the confidence intervals for two groups do not overlap, it suggests a significant difference between the two groups.
Common Misunderstandings
- Not a Guarantee: A 95% confidence interval doesn’t mean there’s a 95% chance the true value is in this range. Instead, it means that if we repeated the sampling many times, 95% of those intervals would contain the true value.
- Wider Confidence Intervals Are Less Precise: As the confidence level increases (e.g., from 95% to 99%), the interval becomes wider. This means we’re more confident the true value is inside, but the precision of the estimate is lower.
- Depends on Sample Size: Larger samples lead to narrower confidence intervals, giving more precise estimates of the population parameter.
In essence, confidence intervals provide a balance between accuracy and precision, helping us make informed guesses about population parameters based on sample data.


Leave a Reply