Probability Theory

Introduction

Probability theory is a branch of mathematics that helps us measure how likely an event is to happen. Imagine you have a coin, and you flip it. It can either land on “heads” or “tails.” Probability theory allows us to figure out the chance of each of these outcomes happening.

Key Concepts in Probability Theory

1. Probability: Probability is the measure of the chance that a certain event will occur. It’s usually represented as a number between 0 and 1:

• 0 means the event is impossible.
• 1 means the event is certain.
• For example, the probability of getting “heads” when flipping a fair coin is 0.5, or 50%, because there are only two possible outcomes: heads or tails.

1. Experiment: In probability, an experiment is any action or process that can lead to different outcomes. Examples include:

• Flipping a coin
• Rolling a die
• Drawing a card from a deck

1. Outcome: An outcome is a single result of an experiment. If you roll a die, there are six possible outcomes (1, 2, 3, 4, 5, and 6). Each number on the die is a different outcome.
2. Event: An event is a collection of one or more outcomes. In the die example, an event could be rolling an even number. The outcomes that make up this event would be 2, 4, and 6.
3. Sample Space: This is the set of all possible outcomes of an experiment. For example, when flipping a coin, the sample space is {heads, tails}. For rolling a die, the sample space is {1, 2, 3, 4, 5, 6}.

Types of Probability

1. Theoretical Probability: This is what we calculate by reasoning or through a formula, without actually performing the experiment. For example, when rolling a fair die, each number has a theoretical probability of 1/6 because there are six equally likely outcomes.

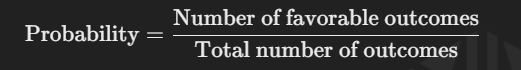
1. Experimental Probability: This is based on the results of an actual experiment. For example, if you flip a coin 100 times and get 48 heads, the experimental probability of getting heads is 48/100 = 0.48.
2. Subjective Probability: This type of probability is based on personal belief or experience rather than on data or mathematical calculations. For example, saying there’s a “high probability” it will rain tomorrow based on your experience with the weather.

Probability Rules

Addition Rule: If two events cannot both happen at the same time (they’re mutually exclusive), the probability of either event occurring is the sum of their individual probabilities.

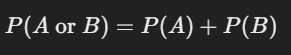
For example, if the probability of rolling a 1 or a 2 on a die is the sum of the probabilities of each outcome:

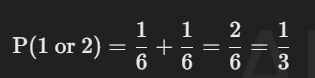
Multiplication Rule: If two events are independent (meaning the occurrence of one event doesn’t affect the other), the probability of both events occurring is the product of their probabilities.

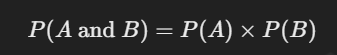
For example, if you flip a coin twice, the probability of getting heads both times is:

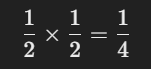
Complement Rule: The probability that an event does not happen is equal to 1 minus the probability that it does happen.

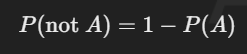
For example, if the probability of rain tomorrow is 0.3, the probability that it won’t rain is:

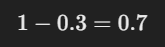
Why Probability Theory is Important

Probability theory is essential in many fields, including finance, engineering, science, and everyday life. It helps us make decisions under uncertainty, understand risks, and predict outcomes. By understanding probability, people can better assess the likelihood of events, plan for the future, and make informed choices.