Econometric Methods:Linear Regression

Introduction

Econometric methods are a set of statistical tools used in economics to analyze data and uncover relationships between different economic variables. One of the most popular and fundamental econometric methods is linear regression. Linear regression helps us understand and predict how one variable (known as the dependent or response variable) changes in response to another variable (called the independent or explanatory variable).

Let’s break down the essentials of linear regression:

1. Understanding Variables in Linear Regression

• Dependent Variable (Y): This is the outcome or the variable we are trying to predict or explain. For example, it could be the sales of a product, a person’s income, or the stock price of a company.
• Independent Variable (X): This is the variable we believe has an impact on the dependent variable. For instance, this could be factors like advertising expenses for sales, years of education for income, or interest rates for stock prices.

2. The Linear Regression Equation

Linear regression assumes that the relationship between the dependent and independent variable can be represented by a straight line. This line can be expressed by the equation:

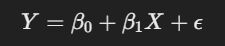
Here’s what each term means:

• Y is the dependent variable.
• X is the independent variable.
• β₀ (Beta 0) is the intercept, the value of Y when X is zero. This represents the starting point of our line.
• β₁ (Beta 1) is the slope, which shows how much Y changes when X increases by one unit.
• ε (epsilon) represents the error term, capturing the effects of all factors that affect Y but are not included in the model. In simple terms, the equation tells us that Y (the outcome) is made up of two parts:
• The predicted part (β₀ + β₁X), which represents what we think Y should be based on X, and
• The error term (ε), which is the part of Y that can’t be explained by X.

3. The Goal of Linear Regression: Finding the Best Fit Line

The aim of linear regression is to find the values of β₀ and β₁ that create the “best fit” line through the data points. This line should minimize the error term ε as much as possible, meaning it should come as close as possible to the actual values of Y for different values of X.

• Ordinary Least Squares (OLS) Method: This is the most common method used to find the best fit line. OLS minimizes the sum of the squared differences (errors) between the observed values and the values predicted by our model. Essentially, it tries to get the line as close as possible to the data points by minimizing the squares of these errors.

4. Interpreting the Results: Slope and Intercept

Once we have the values of β₀ and β₁:

• The Intercept (β₀): This tells us the expected value of Y when X is zero.
• The Slope (β₁): This value is crucial; it shows how much Y is expected to change when X changes by one unit. If β₁ is positive, Y and X have a positive relationship (as X goes up, so does Y). If β₁ is negative, they have an inverse relationship (as X goes up, Y goes down).

5. Goodness of Fit: R-squared

R-squared, or the coefficient of determination, measures how well our linear regression model explains the variation in the dependent variable. It ranges from 0 to 1, where:

• An R-squared of 0 indicates that the model does not explain any of the variation in Y.
• An R-squared of 1 means the model perfectly explains all the variation in Y. For example, if we have an R-squared of 0.8, it means that 80% of the changes in Y can be explained by X.

6. Assumptions of Linear Regression

Linear regression relies on several key assumptions to produce accurate results:

• Linearity: The relationship between X and Y should be linear.
• Independence: The observations should be independent of each other.
• Homoscedasticity: The error term (ε) should have constant variance.
• No Multicollinearity: When using multiple independent variables, they should not be highly correlated with each other.
• Normality of Errors: The error term (ε) should follow a normal distribution.

7. Applications of Linear Regression

Linear regression has widespread applications in various fields:

• Economics: To predict economic indicators like GDP, inflation, or unemployment based on other economic factors.
• Business: To forecast sales based on advertising expenses or market conditions.
• Finance: To estimate asset prices, returns, or the impact of economic policies on financial markets.

8. Limitations of Linear Regression

While powerful, linear regression has limitations:

• It only works well when the relationship between X and Y is linear.
• It can be sensitive to outliers, which are extreme data points that can skew the results.
• It may not perform well when independent variables are highly correlated (multicollinearity).

Example: Simple Linear Regression in Real Life

Imagine we want to study how much people spend on online shopping (Y) based on their monthly income (X). After collecting data on income and spending, we can run a simple linear regression and get the equation:

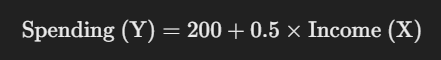
Here, the intercept (200) suggests that even with zero income, the predicted spending is 200 units (perhaps reflecting some base level of spending from savings or credit). The slope (0.5) implies that for each additional unit of income, spending increases by 0.5 units.

In summary, linear regression is a valuable tool in econometrics for predicting and explaining how one variable influences another. By understanding these relationships, economists, business analysts, and data scientists can make informed decisions and predictions.